Convergence analysis of Runge-Kutta methods for ODE IVP#

Evaluation of relative quadrature error with the following parameters:

eq_names = [
    "y'' = -y"          ,
    "y'' = - exp(y)"    ,
    "y'' = xy"          ,
    "y' = Az; z' = By"  ,
]

implicit_methods = {
    f'{rk_name} {order}' : choreo.scipy_plus.multiprec_tables.ComputeImplicitSymplecticRKTablePair_Gauss(order,method=rk_name) for rk_name, order in itertools.product(["Gauss"], [2,4,6,8])
    # f'{rk_name} {order}' : choreo.scipy_plus.multiprec_tables.ComputeImplicitSymplecticRKTablePair_Gauss(order, method=rk_name) for rk_name, order in itertools.product(["Radau_IIA"], [2,3,4,5])
}

explicit_methods = {
    rk_name : getattr(globals()['precomputed_tables'], rk_name) for rk_name in [
            'McAte4'    ,
            'McAte5'    ,
            'KahanLi8'  ,
            'SofSpa10'  ,
    ]
}

scipy_methods = [
    "RK45" ,
    "RK23" ,
    "DOP853" ,
    "Radau" ,
    "BDF" ,
    "LSODA" ,
]

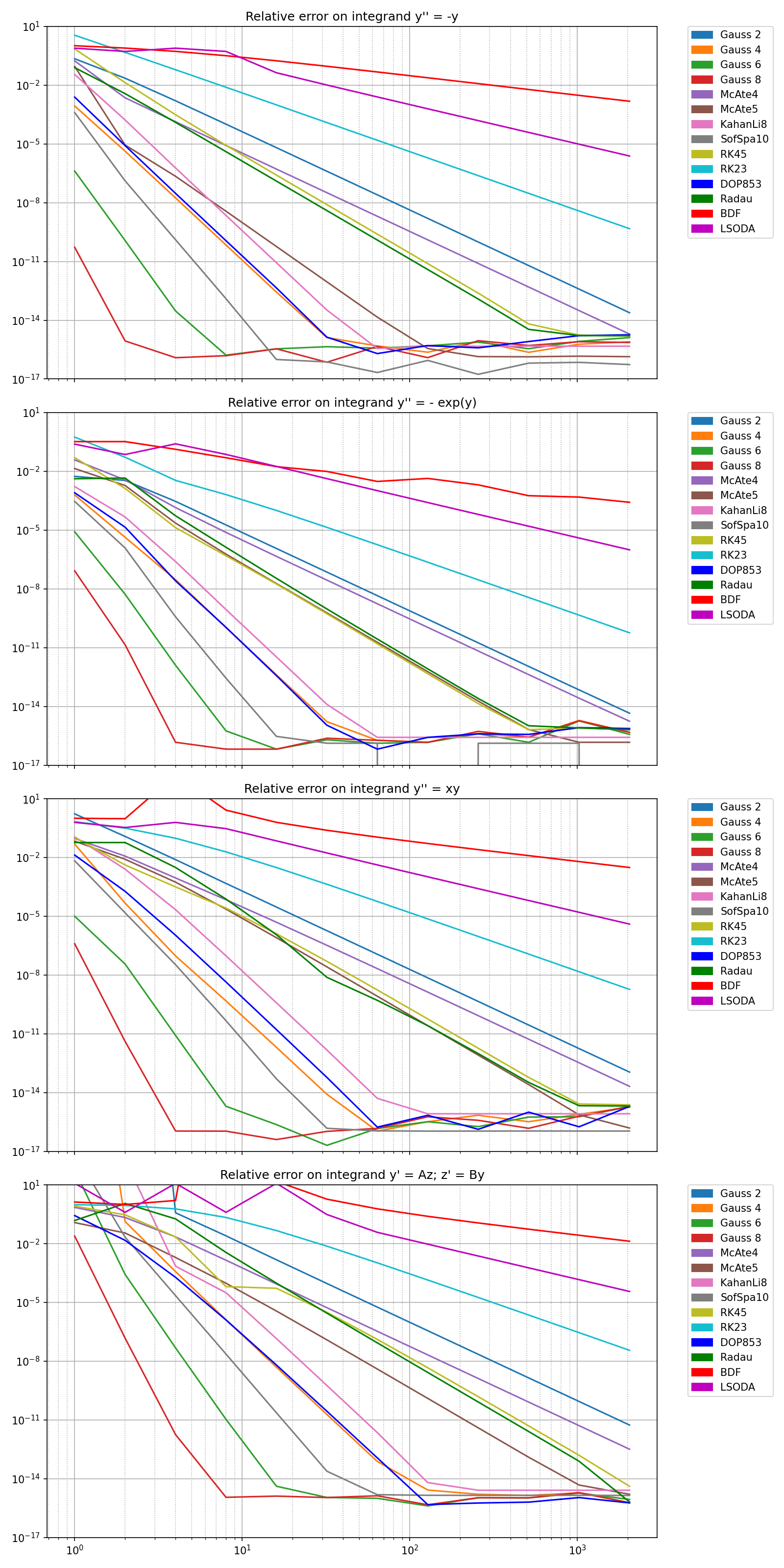
The following plots give the measured relative error as a function of the number of quadrature subintervals

plt.show()

Relative error on integrand y'' = -y, Relative error on integrand y'' = - exp(y), Relative error on integrand y'' = xy, Relative error on integrand y' = Az; z' = By

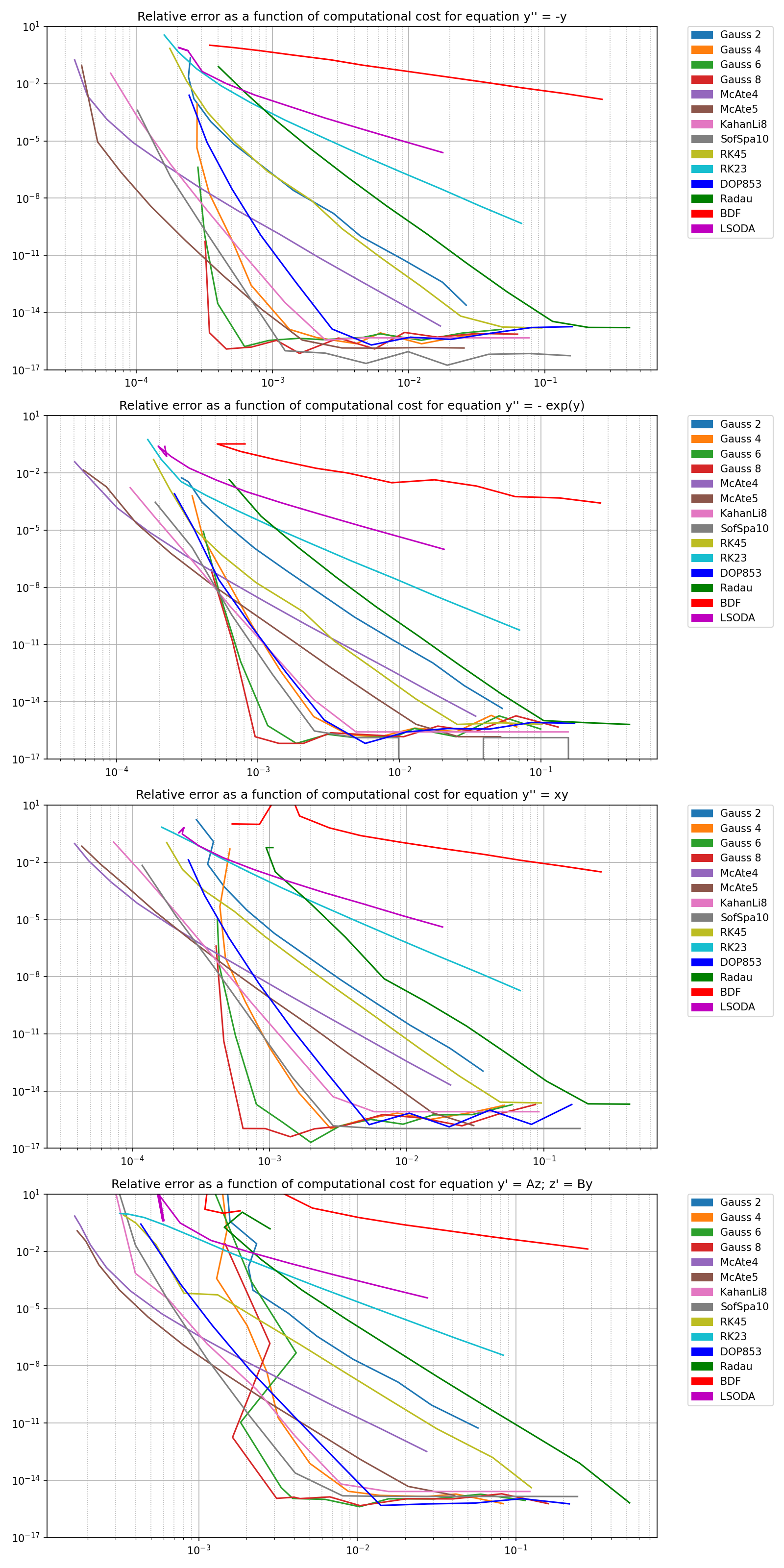
Error as a function of running time

plt.show()

Relative error as a function of computational cost for equation y'' = -y, Relative error as a function of computational cost for equation y'' = - exp(y), Relative error as a function of computational cost for equation y'' = xy, Relative error as a function of computational cost for equation y' = Az; z' = By

Gallery generated by Sphinx-Gallery