Benchmark of FFT implementations available as scipy backends

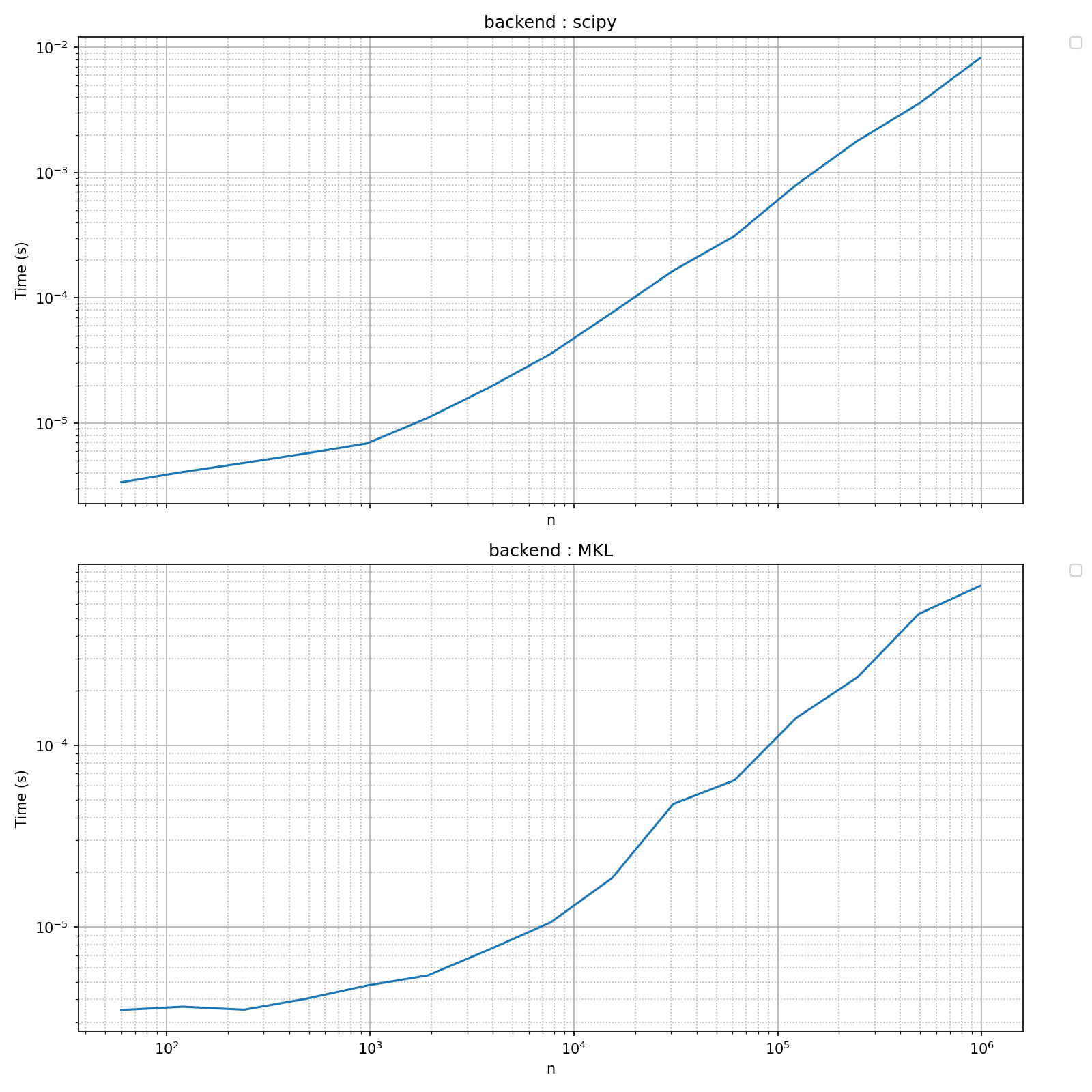
This benchmark compares execution times of several FFT functions using different scipy backends. The plots give the measured execution time of the FFT as a function of the input length. The input length is of the form 3 * 5 * 2**i, so as to favor powers of 2 and small divisors.

def fft(x):
    scipy.fft.fft(x)

def rfft(x):
    scipy.fft.rfft(x)

def dct_I(x):
    N = x.shape[0]
    n = N // 2 + 1
    scipy.fft.dct(x[:n],1)

def dst_I(x):
    N = x.shape[0]
    n = N // 2 - 1
    scipy.fft.dst(x[:n],1)

def dct_III(x):
    N = x.shape[0]
    n = N // 4
    scipy.fft.dct(x[:n],3)

def dst_III(x):
    N = x.shape[0]
    n = N // 4
    scipy.fft.dst(x[:n],3)


all_args = {
    'n' : np.array([4*3*5 * 2**n for n in range(15)])           ,
    'backend' : [backend_name for backend_name in all_backends] ,
}

all_funs = [
    # fft     ,
    rfft    ,
    # dct_I   ,
    # dst_I   ,
    # dct_III ,
    # dst_III ,
]

n_repeat = 10

all_times = pyquickbench.run_benchmark(
    all_args                    ,
    all_funs                    ,
    setup = setup               ,
    n_repeat = n_repeat         ,
    filename = timings_filename ,
    title = 'Absolute timings'  ,
)

plot_intent = {
    'n' : 'points'              ,
    'backend' : 'subplot_grid_y',
}

pyquickbench.plot_benchmark(
    all_times                   ,
    all_args                    ,
    all_funs                    ,
    show = True                 ,
    plot_intent = plot_intent   ,
)

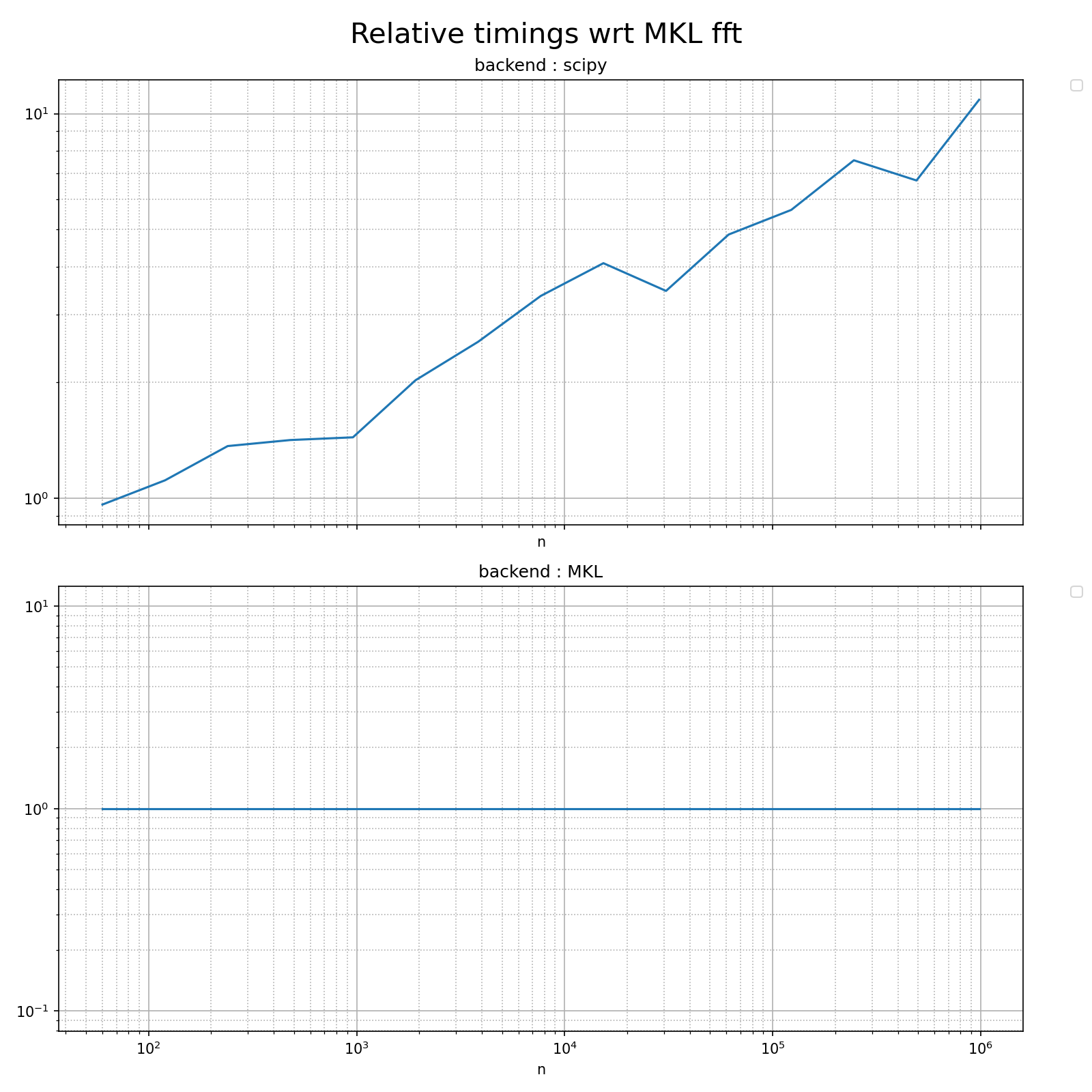
relative_to_val = {
    'backend' : 'MKL'                   ,
    pyquickbench.fun_ax_name : "rfft"    ,
}

pyquickbench.plot_benchmark(
    all_times                   ,
    all_args                    ,
    all_funs                    ,
    show = True                 ,
    plot_intent = plot_intent   ,
    relative_to_val = relative_to_val       ,
    title = 'Relative timings wrt MKL fft'  ,
)