Benchmark of Error-Free Transforms for ODE IVP

This benchmark compares accuracy and efficiency of several summation algorithms in floating point arithmetics for initial value problems of ordinary differential equations

eq_names = [
    "y'' = -y"          ,
    "y'' = - exp(y)"    ,
    "y'' = xy"          ,
    "y' = Az; z' = By"  ,
]

implicit_methods = {
    f'{rk_name} {order}' : choreo.scipy_plus.multiprec_tables.ComputeImplicitRKTable_Gauss(order, method=rk_name) for rk_name, order in itertools.product(["Gauss"], [2,4,6,8])
}

explicit_methods = {
    rk_name : getattr(globals()['precomputed_tables'], rk_name) for rk_name in [
            'McAte4'    ,
            'McAte5'    ,
            'KahanLi8'  ,
            'SofSpa10'  ,
    ]
}

The following plots give the measured relative error as a function of the number of quadrature subintervals

plot_ylim = [1e-17,1e1]

bench_filename = os.path.join(bench_folder, basename_bench_filename+'_error.npz')

all_args = {
    "eq_name" : eq_names                ,
    "nint" : all_nint                   ,
    "DoEFT" : all_EFT                   ,
}

all_errors = pyquickbench.run_benchmark(
    all_args                        ,
    all_funs                        ,
    setup = setup                   ,
    mode = "scalar_output"          ,
    filename = bench_filename       ,
    ForceBenchmark = ForceBenchmark ,
)

plot_intent = {
    "eq_name" : "subplot_grid_y"                ,
    "nint" : "points"                           ,
    "DoEFT" : "curve_linestyle"                 ,
    pyquickbench.fun_ax_name : "curve_color"    ,
}

pyquickbench.plot_benchmark(
    all_errors                              ,
    all_args                                ,
    all_funs                                ,
    mode = "scalar_output"                  ,
    show = True                             ,
    plot_ylim = plot_ylim                   ,
    plot_intent = plot_intent               ,
    title = 'Relative error on integrand'   ,
)

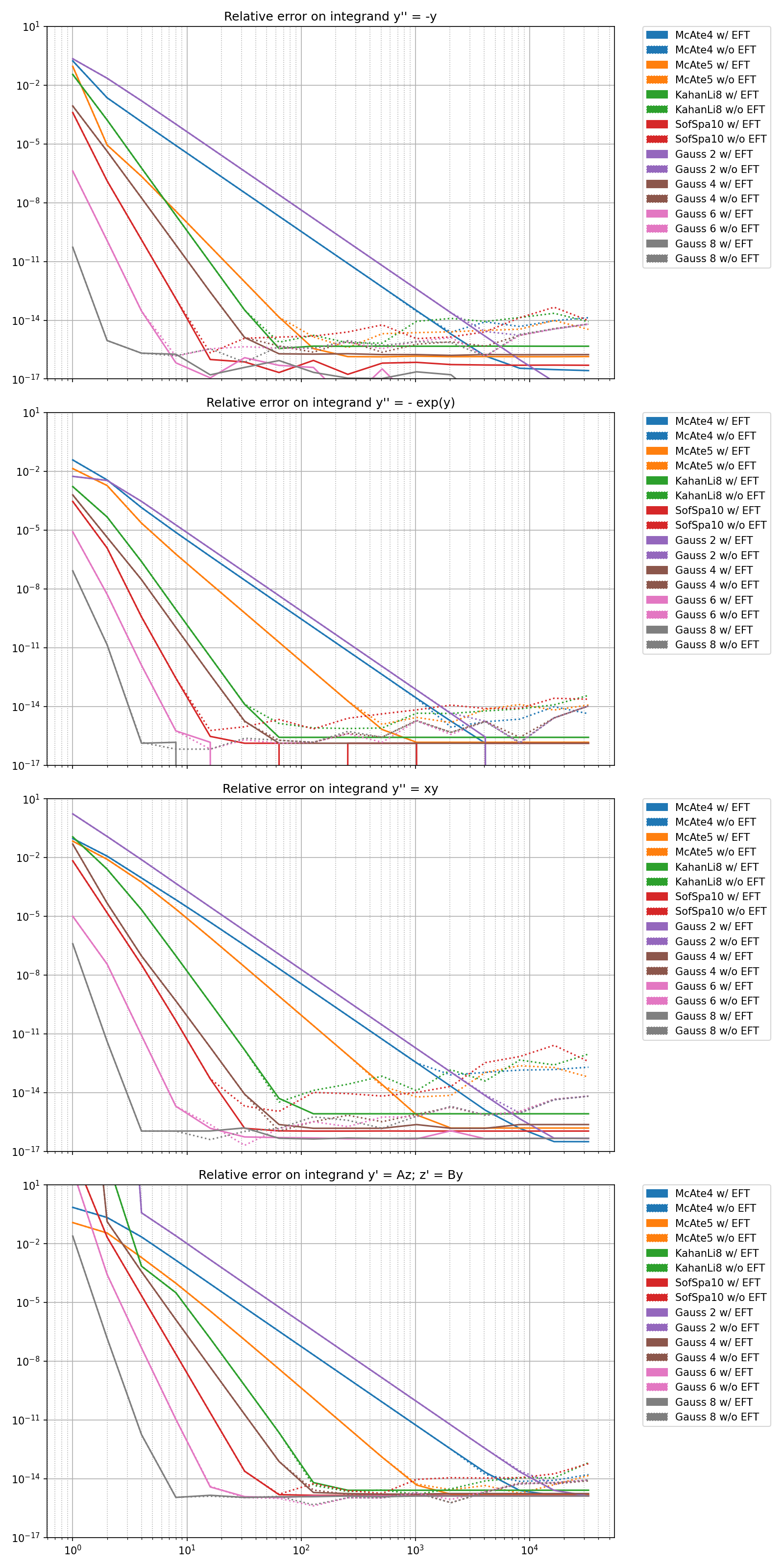
TODO: Add interpretative blabla